Jede Schweizer Postleitzahl verfügt neben weiteren beschreibenden Features über eine Zuweisung zu Längen- und Breitengraden. Für einen schnellen Überblick über die Distanz zwischen den offiziellen Koordinaten von zwei Postleitzahlen lässt sich mit der Haversine-Formel schnell ein passendes Resultat errechnen. Die berechnete Distanz kann helfen, räumliche Daten in Machine-Learning-Modellen als Feature nutzbar zu machen. Prinzipiell ist die Distanz aber auch für andere Anwendungen nutzbar, bei denen ein Set von Längen- und Breitengraden mit einem anderen Set abgeglichen werden soll. Beispielweise könnte man sich alle Wochenmärkte im Umkreis von 50 Kilometern um den eigenen Wohnort ausgeben lassen.

Titel-Image: Louis Hansel on Unsplash

Swiss Open Data

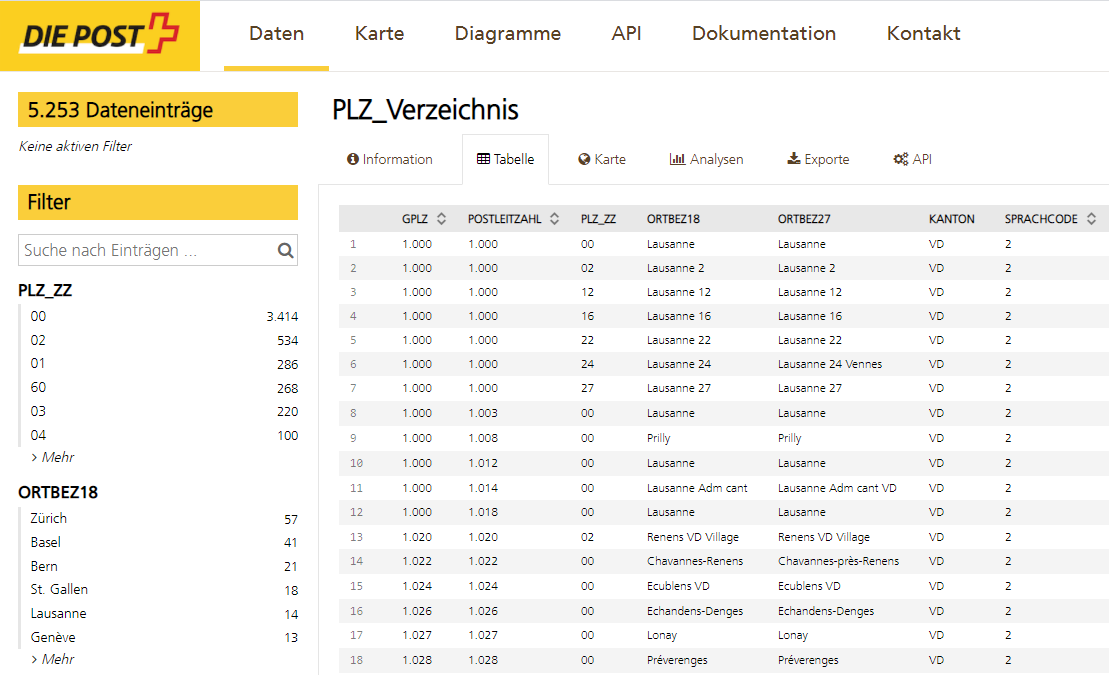
Die Ausgangsdaten für die Implementierung der Distanzen lassen sich aus einem aktuellen Datensatz auf swiss open date beschaffen. Die Schweizerische Post stellt die Daten zur Verfügung und bietet darüber hinaus die Möglichkeit, sich über Updates der Daten informieren zu lassen. So bleiben die verwendeten Daten immer aktuell. Nach dem Einlesen der Daten, sind weiter unten im Script einige Aufbereitungsschritte notwendig, bevor die Daten verwendet werden können.

Haversine-Formel

Die Haversine-Formel beschreibt eine Anwendung der sphärischen Trigonometrie, welche die Seiten und Winkel von sphärischen Dreiecken in Beziehung setzt. Die ersten Tabellen mit diesen Werten findet man im frühen 18. Jahrhundert - verwendet wurden sie für die Navigation. Mit der Formel lässt sich die kürzeste Distanz zwischen zwei Punkten auf einer Kugel unter Verwendung ihrer entlang der Oberfläche gemessenen Längen- und Breitengrade berechnen. Die Ergebnisse sind dahingehend nicht perfekt, das die Berechnung die Annahme trifft, dass es sich bei der Erde um eine perfekte Kugel handele, während sie in Wirklichkeit ein abgeflachter Sphäroid ist. Haversine kann nur auf einer Weltkarte verwendet werden, daher ist Haversine nicht für die Messung von Entfernungen mit anderen Einheiten als Breiten- und Längengrad geeignet. Die Formel lässt sich in vielen Programmiersprachen implementieren, unten sehen wir die Pipeline für einen Pandas Dataframe.

Photo by Nick Seagrave on Unsplash

Code in Python

Nach dem Download der vollständigen PLZ-Informationen für die Schweiz von der Schweizerischen Post müssen die Daten verarbeitet werden. In einem ersten Schritt erfolgen einige Bereinigungen, bevor die Distanzen berechnet und die Ergebnisdaten aufbereitet werden. Der Python-Code für die Datenverarbeitung ist sehr einfach und für weitere Länder oder Beispiele auf Basis von Längen- und Breitengraden verwendbar.

Inputdaten

Von swiss post open data können aktuelle PLZ-Informationen via API bezogen oder als flat file heruntergeladen werden. Um den Code einfacher zu halten, habe ich die Daten zunächst als Excel-File abgespeichert und wie unten beschrieben eingelesen.

import pandas as pd
import numpy as np
import os
import glob
from numpy.lib.scimath import sqrt as csqrt

##########-----------------------------------------------READ RAW DATA

fname = "PLZ.xlsx"
df = pd.read_excel(fname)
df.head(5)

Data Preparation

Wenn wir uns die Daten genauer anschauen, ist zu sehen, dass noch ein paar Zeilen Code in die Aufbereitung der Daten zu investieren ist, bevor die Distanzen sauber berechnet werden können. Zunächst müssen Längen- und Breitengrad getrennt werden, ein Ausschluss doppelter PLZ erfolgen und im letzten Schritt noch ein Teildatensatz mit den Postleitzahlen des Kantons Luzern erstellt werden. Damit sind alle Rohdaten bereit - die Daten aller PLZ der Schweiz inklusive sauberer Längen- und Breitengrade und ein Datenset mit Postleitzahlen, die wir im nächsten Schritt in einen Datensatz mit allen möglichen Kombinationen verwandeln werden.

##########-----------------------------------------------SPLIT LAT/LON, ACCEPT ONLY CORRECTLY FILLED
df['position']=df['Geokoordinaten'].str.rfind(',')+2
df['coor']=df['Geokoordinaten'].str.split(r",", n=-1,expand=False)
df['coor_nr']=df['coor'].str.len()
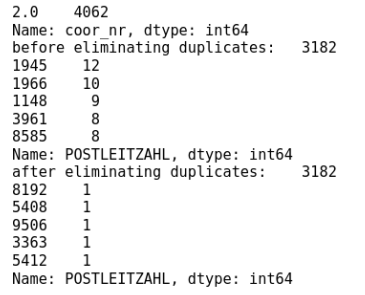
print(df['coor_nr'].value_counts())
df = df[df['coor_nr']==2]
df['lat']= df['coor'].str[0]
df['lon']= df['coor'].str[1]
print('before eliminating duplicaters:   ' + str(df['POSTLEITZAHL'].nunique()))
print(df['POSTLEITZAHL'].value_counts().head(5))
##########-----------------------------------------------DEAL WITH DUPLICATES
df = df.sort_values(by=['POSTLEITZAHL', 'GILT_AB_DAT'])
df['PLZ_duplicated'] = np.where(df['POSTLEITZAHL'].duplicated(), 'Dupe', 'Original')
df = df[df['PLZ_duplicated']=='Original']
print('after eliminating duplicaters:    ' + str(df['POSTLEITZAHL'].nunique()))
print(df['POSTLEITZAHL'].value_counts().head(5))
df.head(5)
 
##########-----------------------------------------------FINAL DATASET
df_final = df[['POSTLEITZAHL','lat','lon']]
fname = "PLZ_coordinates_prep.xlsx"
df_final.to_excel(fname, index=False, sheet_name='PLZ_prep')

##########-----------------------------------------------READ RAW DATA - ONLY LU
df_LU = df.copy()
df_LU = df[df['KANTON']=='LU']
print(len(df_LU))
df_LU.head()
 

Aufbau PLZ-Kombinationen

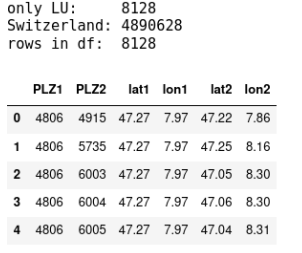
Zunächst ein Exkurs um abschätzen zu können, wie viele Datenzeilen ein Datensatz enthalten wird, der die Kombination aller selektierten Postleitzahlen enthält. Für alle PLZ im Kanton Luzern (128) kommen wir auf 8’182 mögliche Kombinationen, bei denen es keine Dopplungen gibt, die Reihenfolge der zu verwendenden Zahlen nicht beachtet werden soll und immer in Paaren kombiniert wird. Für alle PLZ in der bereinigten Inputdatei (3128) kommen wir auf 4’890’628 mögliche Kombinationen. Mithilfe von itertools lässt sich eine solche Kombinationsliste schnell erzeugen und im Anschluss wieder in einen Pandas-Dataframe umwandeln, der mit den oben erzeugten sauberen Längen- und Breitengraden pro PLZ ergänzt wird.

##########-----------------------------------------------EXCURSE COMBINATIONS
import operator as op
from functools import reduce
 
def ncr(n, r):
    r = min(r, n-r)
    numer = reduce(op.mul, range(n, n-r, -1), 1)
    denom = reduce(op.mul, range(1, r+1), 1)
    return numer // denom
print('only LU:     ' + str(ncr(128,2)))
print('Switzerland: ' + str(ncr(3128,2)))
 
##########-----------------------------------------------GENERATE COMBINATIONS DF
import itertools
input = df_LU['POSTLEITZAHL'].values
output = list(itertools.combinations(input, 2))
df_match = pd.DataFrame(output,
                   columns=['PLZ1', 'PLZ2'])
print('rows in df: ', str(len(df_match)))
 

Distanzberechnung: Haversine-Formel

Die Geo-Informationen ermöglichen uns jetzt mithilfe der Haversine-Formel eine einfache Distanzrechnung innerhalb der PLZ-Paare im Datensatz zu den PLZ im Kanton Luzern zu berechnen. Auch für sonstige Längen- und Breitengrade lässt sich die Formel einfach anwenden. Beispielsweise kann man um den eigenen Wohnort herum berechnen, ob sich spezielle Geschäfte oder andere interessante Orte in einem frei definierten Umkreis befinden. Für das Beispiel der Posteitzahlen im Kanton Luzern könnte eine Fragestellung sein, welche Postleitzahlen die grösstmögliche und welche PLZ die geringsmögliche Distanz zueinander haben. Das Beispiel lässt sich mit wenigen Anpassungen am Script auch für die gesamte Schweiz wiederholen.

##########-----------------------------------------------ADD GEO INFORMATION
df_match = pd.merge(df_match, df_final,
                                  how='left', right_on=['POSTLEITZAHL'],
                                               left_on=['PLZ1'])
df_match = pd.merge(df_match, df_final,
                                  how='left', right_on=['POSTLEITZAHL'],
                                               left_on=['PLZ2'])
df_match = df_match[['PLZ1', 'PLZ2','lat_x','lon_x','lat_y','lon_y']]
df_match.rename(columns = {'lat_x':'lat1','lat_y':'lat2','lon_x':'lon1','lon_y':'lon2'}, inplace = True)
df_match['lat1']=df_match['lat1'].astype(np.float64)
df_match['lat2']=df_match['lat2'].astype(np.float64)
df_match['lon1']=df_match['lon1'].astype(np.float64)
df_match['lon2']=df_match['lon2'].astype(np.float64)
df_match.head()
 
##########-----------------------------------------------haversine distance
df=df_match.copy()
df['rlat1'] = np.radians(df['lat1'])
df['rlon1'] = np.radians(df['lon1'])
df['rlat2'] = np.radians(df['lat2'])
df['rlon2'] = np.radians(df['lon2'])
df['dlon'] =  df['rlon2'] - df['rlon1']
df['dlat'] =  df['rlat2'] - df['rlat1']
df['a'] = np.sin((df['rlat2']-df['rlat1']) / 2)**2 + np.cos(df['rlat1']) * np.cos(df['rlat2']) * np.sin((df['rlon2']-df['rlon1']) / 2)**2
df['c'] = 2 * np.arctan2(np.sqrt(df['a']), np.sqrt(1 - (abs(df['a']))))
df['distance'] = 6371.0 * df['c']
df.head()
 

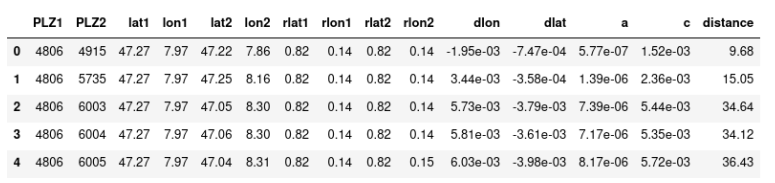
Abschluss und Webressource

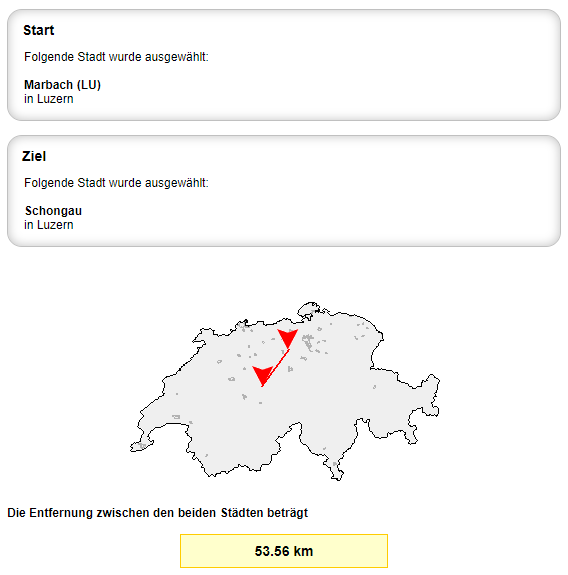
Den Abschluss bildet die Ausgabe der grössten Distanz (km) zwischen zwei Längen- und Breitengraden von PLZ im Kanton Luzern. Die maximale Distanz wird für die Gemeinden Marbach (LU) und Schongau mit 54 km ausgewiesen. Das lässt sich beispielsweise auf postleitzahl.org validieren.

df.loc[df['distance'].idxmax()]

 
fname = "PLZ_haversine_LU.xlsx"
df.to_excel(fname, index=False, sheet_name='LU')

Zusammenfassung

Mit wenigen Zeilen Code und Daten aus swiss open data lassen sich einfache Distanzen für Entfernungsdaten zwischen Längen- und Breitengraden errechnen und in einer Datenbanktabelle ablegen. Diese Daten können dann für Machine-Learning-Modelle verwendet werden, die Distanzen als Feature nutzen möchten. Zusätzlich sind alle möglichen anderen Anwendungsfälle für diese Arten von Daten denkbar, beispielsweise im Sport- oder Freizeitbereich aber auch für Marketingzwecke. Die finalen Daten lassen sich sehr einfach mit Python, Google Spreadsheets und Tableau Public automatisiert in einem Dashboard ablegen. Die Anleitung zum kompletten Ablauf findet sich hier: Python+Google+Tableau. In Tableau Public lässt sich dann ein Dashboard konfigurieren, dass alle Gemeinden der Schweiz, die in einem bestimmten Umkreis um eine Ausgangsgemeinde liegen, einfärbt.

Thank you, and have a beautiful day!